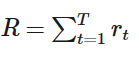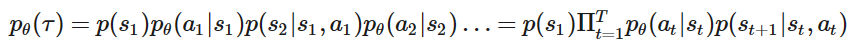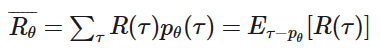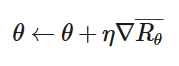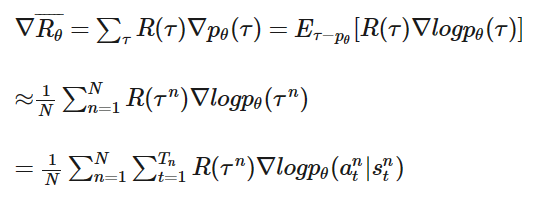强化学习 Learning Walking

First Post:

Last Update:

前言

因为某些现实因素，来学点基础的强化学习内容丰富一下知识库。总体来说挺有趣的，但是搜出来的内容大多用了各种各样复杂的公示，而且有一些门槛，说实话对我这种浅尝辄止的需求有点太过了，以至于大部分文章看着非常晦涩……

在这里自己整理一点相关内容以帮助理解和复习。

这里有些什么知识

出于需求考虑，我需要对强化学习的相关内容有一个大致的理解，包括对相关算法的原理和是实现都能有一定程度上的理解。那么具体来说，本文会记录哪些内容呢？

  • 强化学习概述 - 是什么/怎么做？
  • 马尔可夫决策过程 - 从原理上说，怎么做到的？
  • Q-Learning - 一个案例，具体来说怎么 work？
  • 策略梯度 Policy Gradient

如果你只需要知道强化学习大概是在做什么，那么只需要阅读第一节；而如果你需要知道在理论上是怎么做到的，那么阅读第二节即可；而如果需要知道具体来说代码是怎么实现的，那可以看看第三节。

Walking

强化学习概述

简单来说，强化学习的 “强化” 个人感觉贴近 “自我强化” 的感觉。其主要思想是基于机器人（agent）和环境（environment）的交互学习，其中，环境会返回状态（state）和奖励（reward）。

一个简单的过程是这样的：

环境和机器人都出于初始状态时，机器人通过自己的策略选择一个行为（action）作用到环境上，然后环境根据这个行为返回当前的状态和奖励值。奖励值有可能是正的，也有可能是负的，但机器人的目的是尽可能取得更高的奖励值。

因此接下来，机器人会根据当前的奖励值决定接下来应该采取什么样的行为来提高奖励值。当环境遇到临界状态时（比如撞上死路之类的需要重启游戏的情况），环境和机器人都会重新回到初始状态再开始新一轮尝试，如此往复的过程称之为迭代。在若干轮迭代以后，机器人会选出一个对它来说最优的行动方案，这个行动方案就是我们最终训练出来的模型。

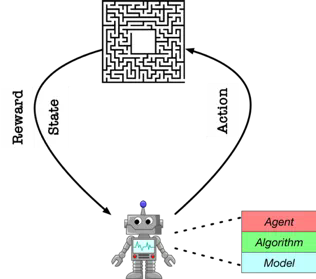
另外，我将状态（state）、时间（time）、行动（action）、奖励（reward）取首字母的星（star）模型表示整个强化学习的理论模型。感觉还挺好记的。

马尔可夫决策过程 Markov Decision Process

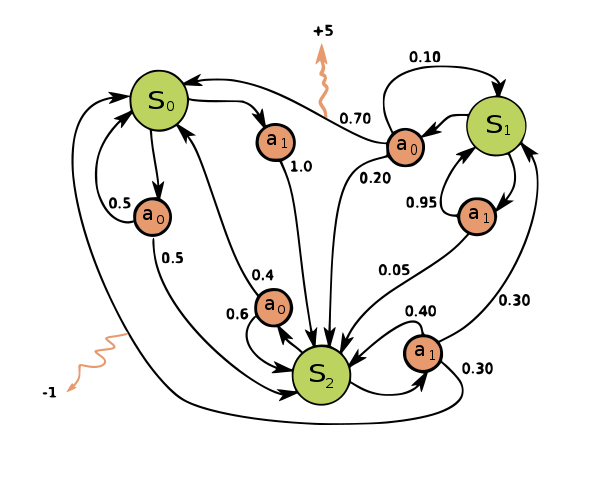
第一节描述的整个过程都是一个马尔可夫决策过程。在概率论中，马尔可夫模型是用于模拟随机变化系统的随机模型。这些模型最显著的特点，就是 “假设未来的状态仅依赖于当前状态，而不依赖于它之前发生的事件”。如果你了解过有限状态机，那差不多就是那种模型。一个状态到另外一个状态的转移只受到当前状态和当前状态发生转移时的概率分布。

马尔科夫链 Markov Chain

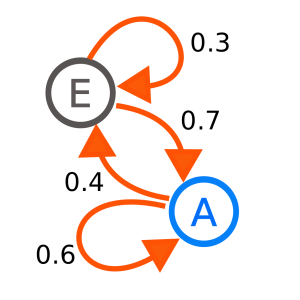
马尔科夫链是最简单的马尔科夫模型。使用马尔科夫性质可以对进行建模。两个状态各自进行转移时只取决于当前状态和概率分布。

隐马尔科夫模型 Hidden Markov Model，HMM


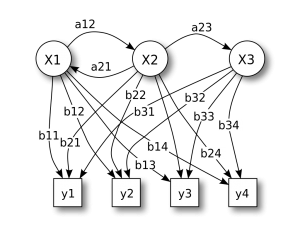
如果系统状态仅能部分观测到，换句话说是只能观察到和系统状态有关但不能直接精确确定系统状态的量。HMM 在语音识别领域中经常被提到，观察到的波形，背后的隐藏状态是文本。

决策过程

在前文描述过一些大致的内容，在这里我们做一些细节上的符号理解。

设当前时间为 t，从状态空间 S 中取出当前状态 st 来表示系统在 t 时刻观测到的状态；而机器人在当前时刻做出行动 at。那么整个系统运行的链条可以通过 s 和 a 来构成：

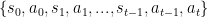
  • 下一个状态是由环境决定的（具体来说应该是由环境和接下来的动作决定的）
  • 下一个动作是由机器人的策略决定的

而前文说过，机器人的目的是尽可能高的取得奖励，将这个策略反应到一个函数上：

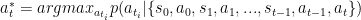
argmax 表示取使函数最大的自变量，星表示最优策略。即表示在历史状态上选出一个最优的行为使得函数最大。

但由于这个模型是马尔科夫过程，也就是影响决策的条件只有当前状态，因此公示里的历史状态就可以简化掉了：

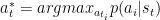
也就是在当前状态下，选出一个使得函数最大的行为。

既然行动决定好了，那么状态转移就好说了：

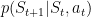
在有限状态机里也有这样的描述，机器人做出行动后，由一定概率跳到某一状态。

奖励、近视远视与贝尔曼方程

在 MDP 模型中，每次从一个状态到另一个状态时，环境会给我们一个返回一个奖励 r。

假设训练过程时间性上无穷的序列，在不停地重复迭代中，我们设置一个减弱的 “打折” 函数，来表示长期的回报：

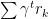
随着未来的步数增长，逐渐指数减弱影响。

设如下函数为依据回报得到的价值函数，根据我们之前设置的 “远视” 系数，可以表示为：

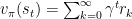
γ用作衰减的系数，其值小于 1，随着时间的增长会衰减，而后面跟着的则是每轮决策的奖励值，这样一来就可以得到从该状态开始未来的期望回报。

但是因为我们训练不可能无穷无尽，必然要在某个时刻被结束，因此再通过贝尔曼方程对上述函数进行简化：



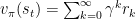
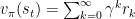
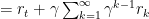
简单来说，在某个状态下的奖励可以分为两个部分，即使奖励和加权后的后续奖励。

即后续奖励=当前状态的奖励+加权后的下个状态开始的后续奖励。

实际上是换了个表现形式，将奖励的迭代只和下一步关联。这样就可以使用迭代函数来求值了，往下参考 Q-Learning。

Q-Learning

Q-Learning 算法是上文所述的MDP模型的一个具体案例。其大致逻辑：

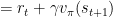
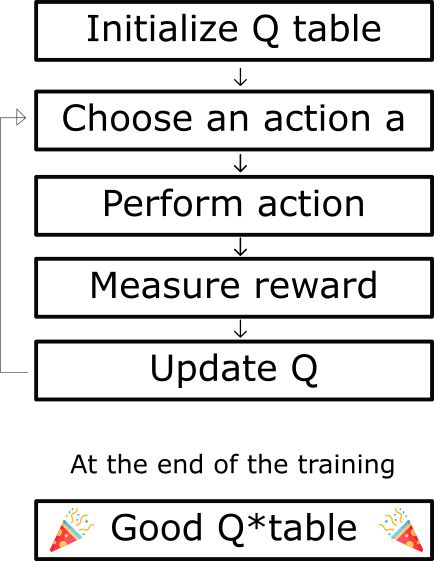
大致来说，这个算法训练的目标是一个名为 Q-Table 的矩阵，流程如下：

  • 初始化 Q-Tabel
  • 选择 Action
  • 施行 Action
  • 评估回报
  • 更新 Q 值

初始化 Q-Table

构造一个m 列（m = 动作数 )，n 行（n = 状态数）的 Q-table，并将其中的值初始化为 0：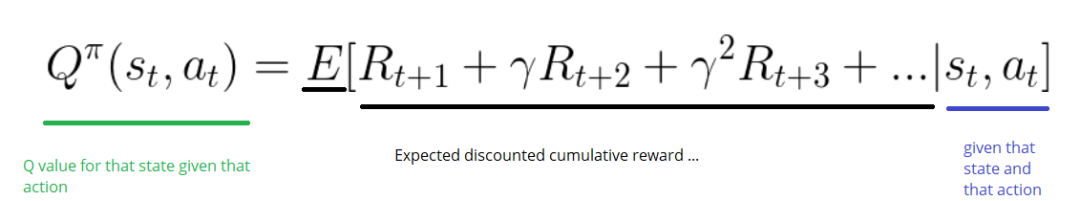

整个模型会通过这个矩阵来表达训练的效果。

选取动作

在基于当前的 Q 值估计得出的状态 s 下选择一个动作 a。

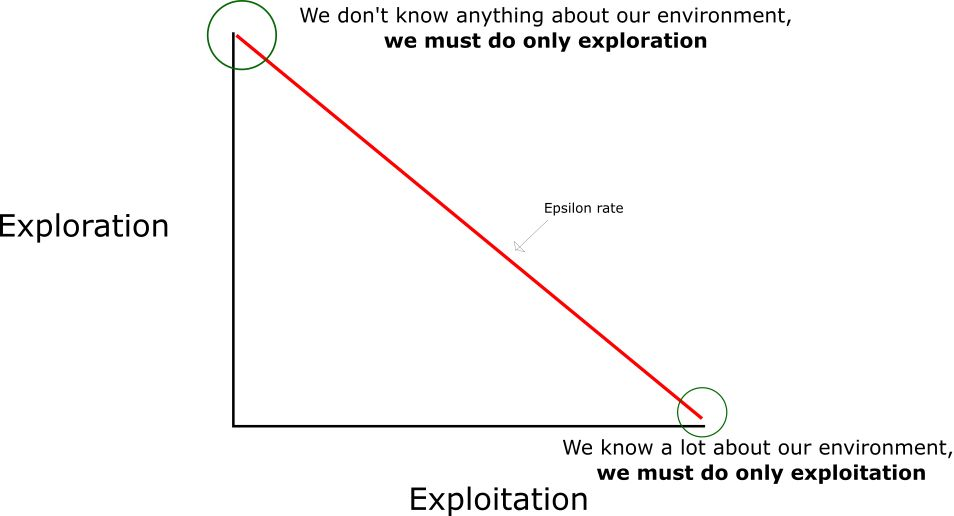
在整个表处于初始状态时，因为目前没有任何能够裁定如何选择动作的方案，因此我们将根据贪婪策略（epsilon）来完成：

  • 我们指定一个探索速率「epsilon」，一开始将它设定为 1。在一开始，这个速率应该处于最大值，因为我们不知道 Q-table 中任何的值。这意味着，我们需要通过随机选择动作进行大量的探索。
  • 生成一个随机数（这里是小数）。如果这个数大于 epsilon，那么我们将会进行「利用」（这意味着我们在每一步利用已经知道的信息选择动作）。否则，我们将继续进行探索。
  • 在刚开始训练 Q 函数时，我们必须有一个大的 epsilon。随着智能体对估算出的 Q 值更有把握，我们将逐渐减小 epsilon。

评估结果

在上述过程中我们完成动作后将从环境得到一个奖励值 r，并更新环境状态为 s’。

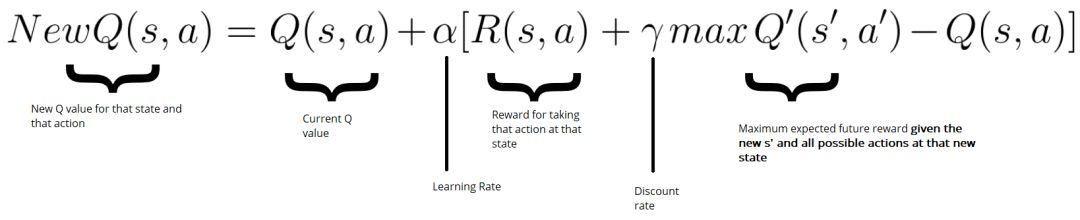
然后使用贝尔曼方程更新 Q-Table：

1
2
3
New Q value = 
   Current Q value + 
   lr * [Reward + discount_rate * (highest Q value between possible actions from the new state s’ ) — Current Q value ]
  • lr：学习速率，一个常量
  • Reward：本次行为的奖励值
  • 这次行动以后，未来预期中最大的 Q Value

一个老鼠吃奶酪的例子：

  • 一块奶酪 = +1
  • 两块奶酪 = +2
  • 一大堆奶酪 = +10（训练结束）
  • 吃到了鼠药 = -10（训练结束）

从起始点，你可以在向右走和向下走其中选择一个。由于有一个大的 epsilon 速率（因为我们至今对于环境一无所知），我们随机地选择一个。例如向右走。

更新 Q 值的流程如下：

唯一理解有点障碍的就是 ΔQ，简单来说就是：本次行动的回报+折算发现速率后在其他选择上得到的现在的 Q 值的最大值 - 这个选择现在的 Q 值。

需要注意的是，这里写的是“现在的”，也就是说，哪怕真的这么行动有可能带来更大的奖励，但因为 Q-Table 还没更新，所以现在也只能得到初始的 0。

策略梯度 Policy Gradient

介绍了上面的 QL（Q-Learning）算法以后，来看看强化学习中的另外一种基础算法。

我们知道 QL 的输入是当前环境的状态和接下来采取的动作，然后输出一个奖励值，然后把该状态下所有的选项试一次，来找到一个奖励最大化的方案。但是这里面有一个明显的问题是，如果这次的行动会影响未来的收益，那么找到的结果永远都只能是局部的，也就是陷入所谓的“局部最优”策略中，贪婪算法往往都有这样的问题。

而 PG（Policy Gradient）的输入是当前环境的状态，输出是动作。但每个动作都是有被执行的概率的，哪怕在当前情况下这个行为没有得到很好的收益，如果在未来带来了更大的收益，那么最终的策略还是会倾向到这个方向。

It turns out that Q-Learning is not a great algorithm (you could say that DQN is so 2013 (okay I’m 50% joking)). In fact most people prefer to use Policy Gradients, including the authors of the original DQN paper who have shown Policy Gradients to work better than Q Learning when tuned well.

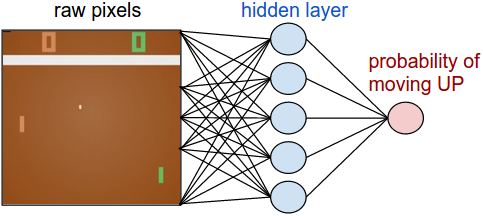
策略网络 Policy Network

策略网络类似于 QL 算法里的策略，只是它综合了环境和决策。

1
2
3
4
h = np.dot(W1, x) # compute hidden layer neuron activations  
h[h<0] = 0 # ReLU nonlinearity: threshold at zero  
logp = np.dot(W2, h) # compute log probability of going up  
p = 1.0 / (1.0 + np.exp(-logp)) # sigmoid function (gives probability of going up)

直观上来说，隐层（W1）提取了图片中的各个特征，比如板子在哪儿，球在哪儿，输出层（W2）则决定了UP和DOWN的概率，所以，在Policy Network中，W1和W2是最重要的参数，我们要训练的就是这两组参数。

基本理论

这个地方基本上套用 Yuang 的博客内容，仅在部分地方加一些注释。个人认为他说的要比我更加清晰易懂，就不再复述了。

对于一个强化学习问题，这个问题的基本对象有这些：Actor、Environment、Reward Function。

举个例子，AlphaGo下围棋的问题，Actor是AlphaGo，Environment是对手和棋盘，Reward Function基于围棋的规则。再举个栗子，我们玩电子游戏，手柄是Actor，电脑屏幕或者游戏机是Environment，Reward Function是杀死敌人或者占领据点（还是依据游戏规则）。其中Environment和Reward Function是我们无法在训练过程中改变的，只有Actor是受控的。

那么如何控制Actor？

我们对Actor的控制，需要策略，而策略我们用 𝜋 符号表示。

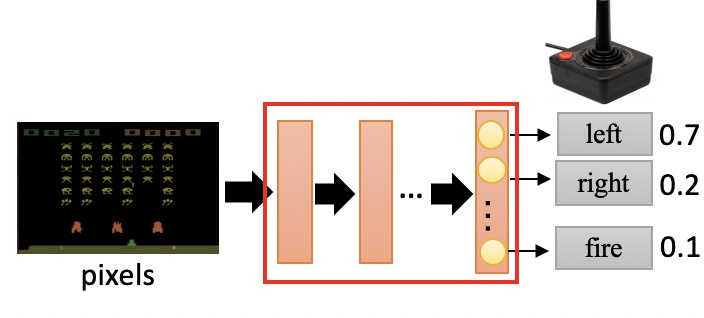
𝜋 是一个参数为 𝜃 的神经网络，输入是 observation（矩阵）；输出是数量为 𝑛 的神经元。

observation是给神经网络提供当前状态的参数，我们可以把游戏的当前图像作为observation，这时observation实际上是一串像素，我们也可以直接把各种参数作为observation，比如说我和敌人的距离、我方英雄技能的攻击范围。总之，observation提供了当前状态的特征。

输出的每个神经元代表一个动作，神经元包含的值表示这个动作的发生概率。

我们按照概率来选择动作，概率高的自然梗容易被选择，并在选择后计算动作的奖励，第𝑖个动作𝑎𝑖的reward用𝑟𝑖表示。

此处所说的参数 𝜃 在文中并没有描述，根据我自己的理解，我们可以把他当作对策略网络的定义。对于不同的参数，有不同的神经网络，而训练的目的就是找到一个合适的参数，令这个神经网络的效果最佳。因此找到这个参数就是我们的目标，更进一步说，找到这个神经网络就是我们的目的。在这里只需要把他当作一个用于定义神经网络各个属性的参数即可。

以电脑游戏为例

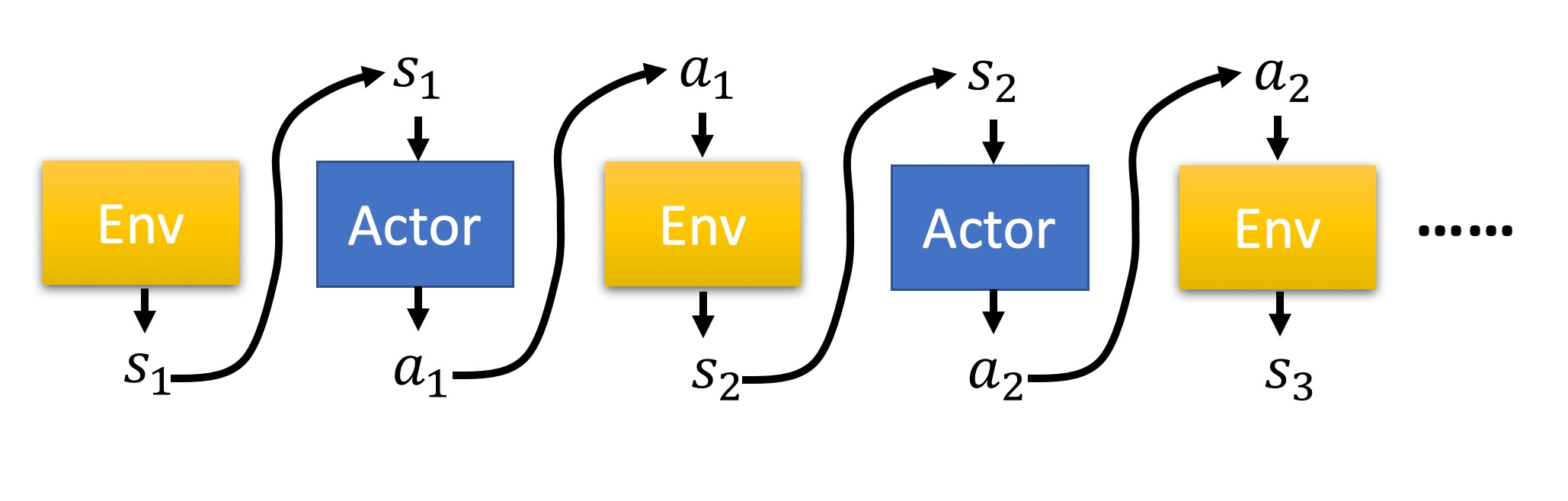
比如说我们玩一个电脑游戏，游戏现在的状态是𝑠1，然后 𝜋 选择了动作𝑎1，游戏照做了，然后我们计算一个reward 𝑟1；游戏在执行了动作𝑎1后的状态为𝑠2，然后我们再选择了动作𝑎2，执行动作后，计算了一个reward 𝑟2，这样一直下去，直到游戏结束（游戏赢了或者输了）。

截止游戏结束，我们一共选择了𝑇个动作，计算出了𝑇个reward，这一回合我们称之为一个episode，一个episode的整个reward是每个动作的reward之和：


这整个episode是Environment、Actor之间的交互，在episode中产生了一串环境与动作的序列，叫做Trajectory（轨迹）。

Trajectory τ=s1,a1,s2,a2,…,sT,aT

我们可以算出整个trajectory的概率𝑝𝜃(𝜏)

注：当前策略网络中，出现轨迹 τ 的概率为 pθ(τ)

有一点很重要，虽然在episode中，𝜃是确定的，但是Environment是不受我们控制的，所以即使在相同的𝜃下，游戏状态𝑠𝑖是不受控的，所以在不同的状态下，产生出的trajectory也会不同。所以要求在 𝜃 下的Reward，我们需要求R的期望Expectation

我们的目的很明确很简单，就是调整𝜃把𝑅𝜃 最大化，下面就是我们常用的梯度下降（Gradient Descent）


其中：


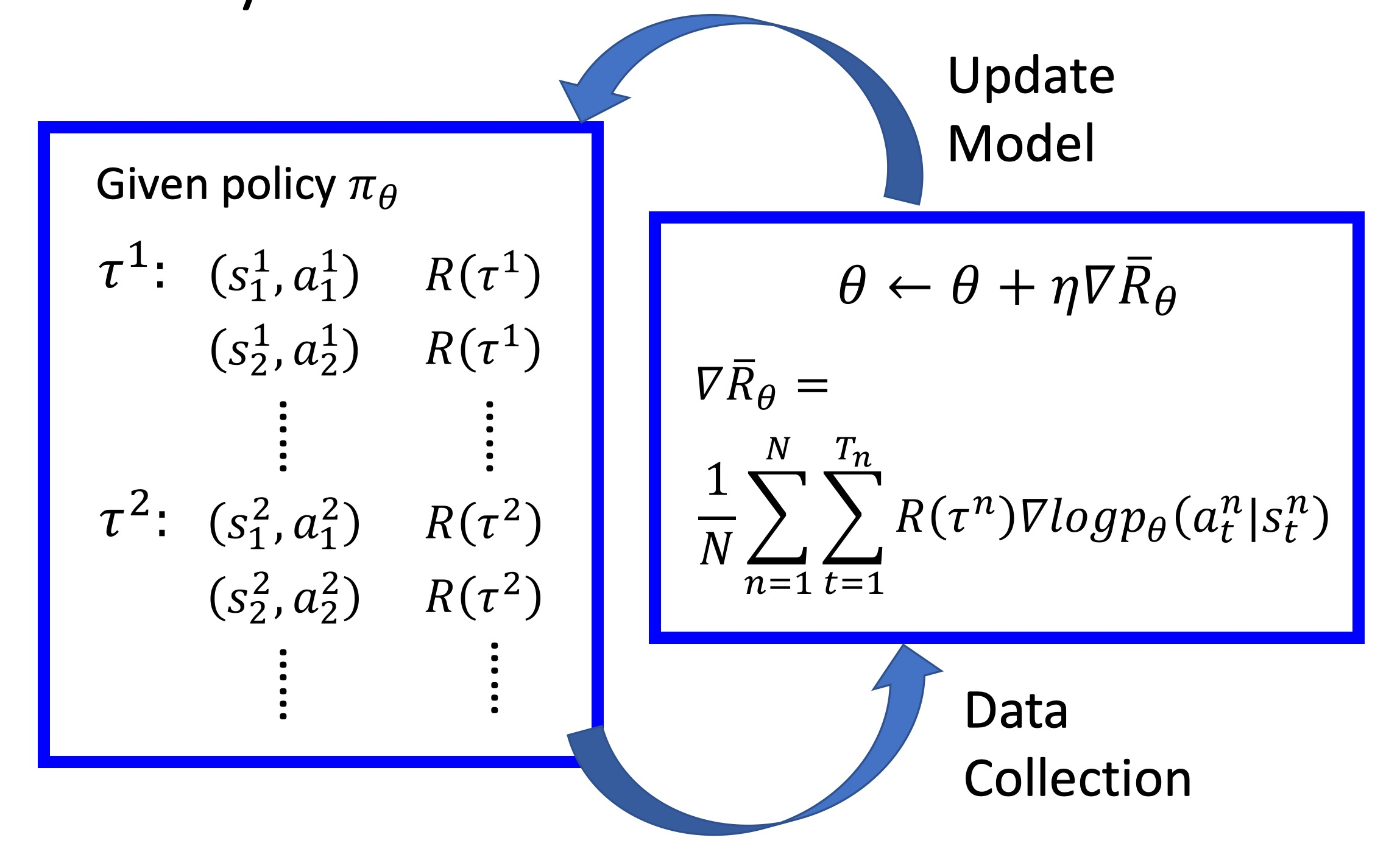
整个过程如图：

在𝑁个episode中，我们要记录每一个𝜏𝑛中的序列对(𝑠𝑖𝑛,𝑎𝑖𝑛)，记录𝜏𝑛的reward𝑅(𝜏𝑛)，然后对𝜃进行更新。

异步优势A3C

这部分就不再复制粘贴了，这份博客写的非常详细，连我这种没入门的人都能看得懂了：
https://www.cnblogs.com/wangxiaocvpr/p/8110120.html

这里就提一句我比较在意的内容：为什么说A3C算法是综合了 QL 和 PG 两个算法？

个人认为 QL 和 PG 的最明显的区别在于，QL 使用的是贪婪算法，它总是要去尽可能的测量所有行为的奖励，并籍此选出最合适的方案；而 PG 则引入了神经网络的方案，输出给出的不是确定的行动而是一组概率分布，并通过计算策略的梯度来优化未来输出的概率分布。

那么在 Actor-Critic 算法中把这两个结合一下，通过 PG 算法来优化概率分布，再通过 QL 算法的方案来评估预期的奖励，选取奖励最大化的策略。

简单来说就是，在 QL 的算法中本来是只有 Critic 的，由一个 agent 来选取行为；而在 PG 的算法中是只有 actor 的，通过优化策略来提高效果。接下来把这两个角色凑到一起组成新的网络，一个负责输出 action 并自己学习优化策略，另外一个负责评价，提高精度。

至于 A3C，其实就是把 AC 算法再拓展到异步去，在计算机实现里也就是多任务（多进程/多线程）了。因为AC算法其实是在针对一份材料进行训练的，也就是说最终效果有可能会特化为对该材料特攻，所以用 A3C 算法让它同时针对多份不同材料进行训练，然后汇总到一起，以消除这个问题。

参考文章

https://www.jiqizhixin.com/articles/2019-02-20-8
https://steinslab.io/archives/1621
https://www.jiqizhixin.com/articles/2018-04-17-3
https://yuuuuang.com/2018/11/03/Policy-Gradient/
https://zhuanlan.zhihu.com/p/107906954
https://www.cnblogs.com/wangxiaocvpr/p/8110120.html

≡