学习过程跟进《数据结构与算法分析》,主要代码大致与树种例程相同,若有疏漏或错误,请务必提醒我,我会尽力修正。
目录:
- [toc]优先队列(堆)
- 最小堆HeapMin
- 左式堆Leftist Heap
- 二项队列Binomial-Queue
优先队列(堆):
一种能够赋予每个节点不同优先级的数据结构。有“最小堆”和“最大堆”两种基础类型。实现的根本原理有两种,一种是“数组”,另外一种则是“树”(大多是指二叉树)。但在实现最大/最小堆时,使用数组更优。因为堆并不像树那样需要很多功能支持,自然也不需要用到指针(当然,高级结构还是会用到的,比如“左式堆”等,之后将有实现)。
如果您此前已经看过堆的基本结构概念,那应该大致明白最小堆长什么样了,基础结构的堆就是一颗符合特定条件的二叉树罢了。
特殊性质:对每一个节点的关键字,都要比其子树中的任何一个关键字都小(任何一个节点的关键字是其子树以及其自身中最小的那个)。这个条件是针对最小堆的,最大堆则反之。
因为基础的堆结构只支持“插入”和“最小值出堆”这两种操作。在处理任务进程的时候,对应的也有“增加任务”和“处理任务量最少的任务”这种解释,或许这样更容易让人明白堆的作用。而最大堆则可将其解释为“处理优先级最高的任务”。(当然,实际上还需要对任务量/优先级进行变动,包括增/减关键字的大小这样的操作,自然也能够进行特定关键字的删改了)。
最小堆HeapMin:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| //-----------声明部分----------//
struct HeapStruct;
struct ElementType;
typedef struct HeapStruct* PriorityQueue;//堆指针
#define MinElements 1
#define Max 99999
bool IsEmpty(PriorityQueue H);//是否为空堆
bool IsFull(PriorityQueue H);//是否为满堆
void Insert(ElementType key, PriorityQueue H);//插入关键字
ElementType DeleteMin(PriorityQueue H);//删除最小值
PriorityQueue BuiltHeap(ElementType* Key, int N);//成堆
void PercolateDown(int i, PriorityQueue H);
PriorityQueue Initialize(int MaxElements);//建空堆
void IncreaseKey(int P, int Add, PriorityQueue H);//增加关键字值
void DecreaseKey(int P, int sub, PriorityQueue H);//降低关键字值
void Delete(int P, PriorityQueue H);//删除关键字
struct ElementType//关键字数据块
{
int Key;
};
struct HeapStruct//堆结构
{
int Capacity;
int Size;
ElementType* Element;
};
ElementType MinData;//最小数据块
//-----------声明部分----------//
|
看注释大概就能明白了。但值得说明的是,因为最终是通过数组来实现的,而数组必须先行规定好它的尺寸,所以建立的堆也必须面临“被装满”的情况(当然,用new函数重新开辟也行,谁让这是C++呢)
建立空堆Initialize:
1
2
3
4
5
6
7
8
9
10
11
12
| PriorityQueue Initialize(int MaxElements)//形参为堆的总节点数
{
PriorityQueue H;
if (MaxElements < MinElements)
return NULL;
H = new HeapStruct;
H->Element = new ElementType[MaxElements + 1];
H->Capacity = MaxElements;
H->Size = 0;
H->Element[0] = MinData;
return H;
}
|
注:我并没有把new函数失败的情形写出来,但那些内容并不影响对数据结构的学习。对这方面有需求请自行添加。
注:MinData是一个最小数据块,同时也只是一个冗余块。在之后的任何操作中,都不会对存有MinData的Element[0]进行任何操作。只是通过占用[0]节点,使得之后的操作变得更加可行了。需要注意的是,这个0节点并不是根节点(当时没绕过来,在这里浪费了太多时间)。
插入Insert:
1
2
3
4
5
6
7
8
9
10
| void Insert(ElementType key, PriorityQueue H)
{
int i;
if (IsFull(H))
exit;
++H->Size;
for (i = H->Size; H->Element[i / 2].Key > key.Key; i /= 2)
H->Element[i] = H->Element[i / 2];
H->Element[i] = key;
}
|
for循环中的判断方式被称之为“上滤”,也是这种方式得以实现的重要规则。对于根节点从 Element[1] 开始的这个堆,Element[i]的左儿子必然是Element[2*i],除非它没有左儿子。
回到这个函数,因为int型会自动取整舍弃小数位,所以 Element[i/2] 必定指向 Element[i] 的父节点,不论它是不是单数。
而这个寻路条件则是在不断的比较子节点与父节点的大小。流程如下:
①先将新节点放在数组的最后一位(并不是指数组的末尾,而是按照顺序装填的最后一位),然后比较它与父节点的大小。
②若它小于父节点,那么将其与父节点交换位置,此时 i/=2 , Element[i]再次指向它。
③继续相同操作。直到父节点小于它,或是没有父节点为止。
不得不承认,这种操作很棒。因为它让函数的最坏时间复杂度降到了logN(因为实际操作中,不一定都要上履到最顶层)。
最小值出堆DeleteMin:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| ElementType DeleteMin(PriorityQueue H)
{
int i, Child;
ElementType MinElement, LastElement;
if (IsEmpty(H))
return H->Element[0];
MinElement = H->Element[1];
LastElement = H->Element[H->Size--];
for (i = 1; i * 2 <= H->Size; i = Child)
{
Child = 2 * i;
if (Child != H->Size && H->Element[Child + 1].Key < H->Element[Child].Key)
Child++;
if (LastElement.Key > H->Element[Child].Key)
H->Element[i] = H->Element[Child];
else
break;
}
H->Element[i] = LastElement;
return MinElement;
}
|
同“上滤‘相近,在这个函数中运用的方法为”下滤“。简要谈谈过程吧:
①声明各种各样的变量,并判断H是不是一个空堆。
②将堆中最小的值Element[1]拷贝到MinElement中,同理将最后一个值放进LastElement中。(这个Element[1]将会被新值替换,而这个LastElement则要用来填补某个空缺)
③从i=1开始,Child则指向根节点Element[1]的左儿子,同时比较根节点的左右儿子大小,将Child指向小的那一个,我是说,H->Element[Child]会指向小的那个。
④然后再判断最后一个数和 H->Element[Child] 的大小。如果最后一个比较大,那就把父节点Element[i]用它的子节点替代。
⑤重新回到循环,现在的 i 已经指向了本来的子节点,并开始重复上述从③开始的操作,直到当前Element[i]的子节点中较小的那一个Element[Child]比最后一个节点的值要小为止。
⑥将现在的父节点Element[i]用最后一个替代。
或许从途中就会觉得有些怪异,这究竟是个怎么回事。
事实上,经过上述操作直到步骤⑤,最终的Element[i]将会指向某片叶子,这片叶子是根据其上的操作逐层筛选出来的。最后通过
1
| H->Element[i] = LastElement;
|
将这个位置用最后一位来替代,并返回了刚开始拷贝好的最小值,实现了删除最小值的操作。当然,实际上,这个数组的最后一位仍然保存着某个关键字,但并不需要太担心,因为经过了H->Size–,当下次插入节点的时候,遇到合适的数值,将会直接把这个位置覆盖掉。并且,也如您所见,所有的操作单元均在[1,H->Size]的范围内,对于范围外的元素,即便它还留有关键字,也不会再造成影响了。
成堆BuiltHeap:
通常,我们将会导入一整串数组,然后再利用它们来生成一个堆结构。实际上,当然也可以通过Insert来一个个安置。以下是没套用Insert的例程,主要通过递归来实现。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| PriorityQueue BuiltHeap(ElementType *Key,int N)//Key指向将要导入的数据数组
{
int i;
PriorityQueue H;
H = Initialize(N);
for (i = 1; i <= N; i++)
H->Element[i] = Key[i - 1];
H->Size = N;
for (i = N / 2; i > 0; i--)
PercolateDown(i, H);
return H;
}
void PercolateDown(int i,PriorityQueue H)
{
int MinSon;
ElementType Tmp;
if (i <( H->Size / 2))
{
if (2 * i + 1 <= H->Size && H->Element[2 * i].Key > H->Element[2 * i + 1].Key)
MinSon = 2 * i+1;
else
MinSon = 2 * i;
if (H->Element[i].Key > H->Element[MinSon].Key)
{
Tmp = H->Element[i];
H->Element[i] = H->Element[MinSon];
H->Element[MinSon] = Tmp;
}
PercolateDown(MinSon, H);
}
}
|
①声明,并建立空堆,然后把所有元素全都不按规则的塞进去,再指定好H->Size。
②从最后一个具有“父节点”性质的节点进入下滤函数。过程与DeleteMin相近:选出子节点中小的,再与父节点比较,将较小的那一个放在父节点的位置,而较大的那一个下沉到子节点。并且再次进入这个函数。
③实现全部的过滤之后,返回H。
递归在这里是非常好用的。在BuiltHeap函数中,for循环实现了对每一个具有“父节点”性质的节点进行下滤(这是根据数组节点的排列顺序实现的,父节点必然都能按顺序排下去)。而递归则实现了对整条路径的下滤操作。假设从根节点开始下滤,那么必然会进入PercolateDown(MinSon,H)中,将较小的那个子节点作为本次递归的新的父节点同样进行下滤。最终实现了堆序(Heap order)。
剩下的就是一些无关紧要的函数了,看看思路就行。因为是我自己写的,可能会有错误,如有发现,还请务必告知我,我会尽量修正。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| void DecreaseKey(int P,int sub,PriorityQueue H)//降低关键字的值
{
H->Element[P].Key -= sub;
int i;
ElementType Tmp;
for (i = P; H->Element[i / 2].Key > H->Element[i].Key; i /= 2)
{
Tmp = H->Element[i / 2];
H->Element[i / 2] = H->Element[i];
H->Element[i] = Tmp;
}
}
void IncreaseKey(int P, int Add, PriorityQueue H)//提高关键字的值
{
int i,Child;
ElementType Tmp;
H->Element[P].Key += Add;
for (i = P; 2 * i <= H->Size; i = Child)
{
Child = 2 * i;
if (Child != H->Size && H->Element[Child + 1].Key < H->Element[Child].Key)
Child++;
if (H->Element[i].Key > H->Element[Child].Key)
{
Tmp = H->Element[Child];
H->Element[Child] = H->Element[i];
H->Element[i] = Tmp;
}
else
break;
}
}
void Delete(int P,PriorityQueue H)//删除指定关键字
{
DecreaseKey(P, Max, H);
DeleteMin(H);
}
|
原理同上面的其他函数一样的,建议自己实现一下。
左式堆Leftist Heap:
因为基础的堆结构由数组实现,所以并不支持合并等高级操作(有办法实现,但效率并不那么理想),为解决这些问题,左式堆提供了一些方案。
左式堆同样遵守最小堆的基本堆序——任意节点的关键字值低于其子树中的所有节点,但与之不同的是,左式堆的基本结构还包含了Npl(Null path length),即从该结点到达一个没有两个孩子的结点的最短距离。并要求:任意结点的左孩子的Npl大于或等于右孩子的Npl。
声明部分:(函数对应的作用已经写在注释里了)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| //----------声明部分----------//
typedef struct TreeNode* PriorityQueue;//节点指针
struct TreeNode//节点结构
{
int Element;
PriorityQueue Left;
PriorityQueue Right;
int Npl;//Null Path Length
};
PriorityQueue Initialize(void);//建立空堆
PriorityQueue Merge(PriorityQueue H1, PriorityQueue H2);//合并堆(驱动例程)
static PriorityQueue Merge1(PriorityQueue H1, PriorityQueue H2);//合并堆(实际例程)
void SwapChildren(PriorityQueue H);(交换H的左右子树)
PriorityQueue Insert1(int key, PriorityQueue H);//插入节点
bool IsEmpty(PriorityQueue H);//是否为空堆
PriorityQueue DeleteMin1(PriorityQueue H);//删除最小值
//----------声明部分----------//
|
建立空堆Initialize:
1
2
3
4
5
6
7
8
| PriorityQueue Initialize(void)
{
PriorityQueue H;
H = new TreeNode;
H->Left = H->Right = NULL;
H->Npl = 0;
return H;
}
|
规定NULL的Npl为-1,则对任何一个没有两个子树的节点,其Npl为0。
插入Insert:
1
2
3
4
5
6
7
8
9
10
| PriorityQueue Insert1(int key, PriorityQueue H)
{
PriorityQueue SingleNode;
SingleNode = new TreeNode;
SingleNode->Element = key;
SingleNode->Npl = 0;
SingleNode->Left = SingleNode->Right = NULL;
H = Merge(SingleNode, H);
return H;
}
|
区别于最小堆中的Insert函数,这里用的是Insert1。因为Insert没有返回值,也不需要返回值,所有那样做是没有问题的;但在左式堆中,将一个元素插入空堆时,需要返回新的根节点地址,所以应有一些区别。另外,这个函数首次出现了Merge函数。关于Merge函数将会放在最后,目前权且当它是一个合并两个堆,并返回新的根节点的函数即可。(目前我个人还不会写宏定义,但如果您已经学会了,不妨试着将Insert函数写成宏定义,书上是这样建议的)
删除最小值Delete:
1
2
3
4
5
6
7
8
| PriorityQueue DeleteMin1(PriorityQueue H)
{
if (IsEmpty(H))
exit;
PriorityQueue LeftHeap=H->Left, RightHeap=H->Right;
delete H;
return Merge(LeftHeap, RightHeap);
}
|
因为左式堆和最小堆有着同样的结构,所以最小值同样都是根节点,所以例程非常的简洁也很清晰。已经没必要做其他解释了。
合并堆Merge:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| PriorityQueue Merge(PriorityQueue H1, PriorityQueue H2)//驱动例程
{
if (H1 == NULL)
return H2;
if (H2 == NULL)
return H1;
if (H1->Element < H2->Element)
return Merge1(H1, H2);
else
return Merge1(H2, H1);
}
static PriorityQueue Merge1(PriorityQueue H1, PriorityQueue H2)//实际例程
{
if (H1->Left == NULL)
H1->Left = H2;
else
{
H1->Right = Merge(H1->Right, H2);
if (H1->Left->Npl < H1->Right->Npl)
SwapChildren(H1);
H1->Npl = H1->Right->Npl + 1;
}
return H1;
}
void SwapChildren(PriorityQueue H)//交换子树
{
PriorityQueue Tmp;
Tmp = H->Left;
H->Left = H->Right;
H->Right = Tmp;
}
|
最后是关键的合并堆函数。Merge函数作为合并开始的入口被调用,而实现过程则放在Merge1函数中进行。SwapChildren函数是附带的,你当然也可以把它写在Merge1中。
对于没有图的过程描述,我觉得实在有些难以想象。这里引用书上的例子(尽管这个例子并不方便,但在某些地方能起到很好的范例)。
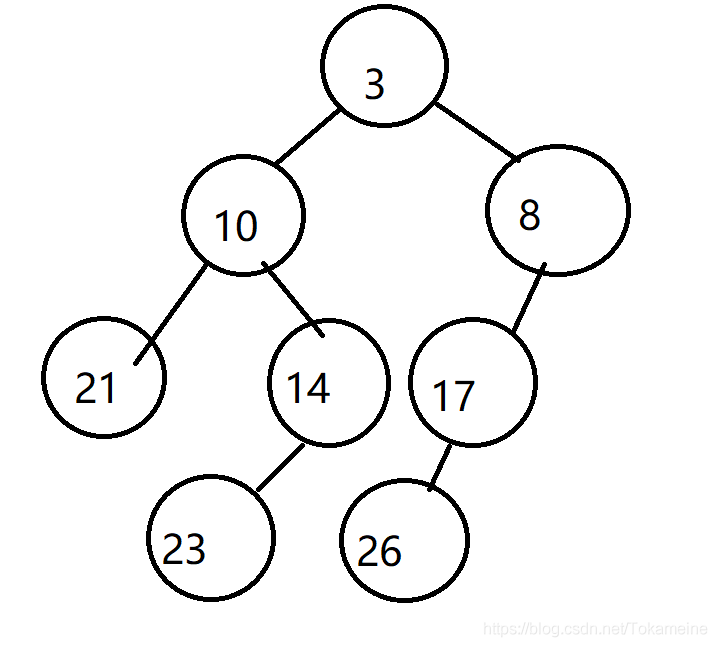
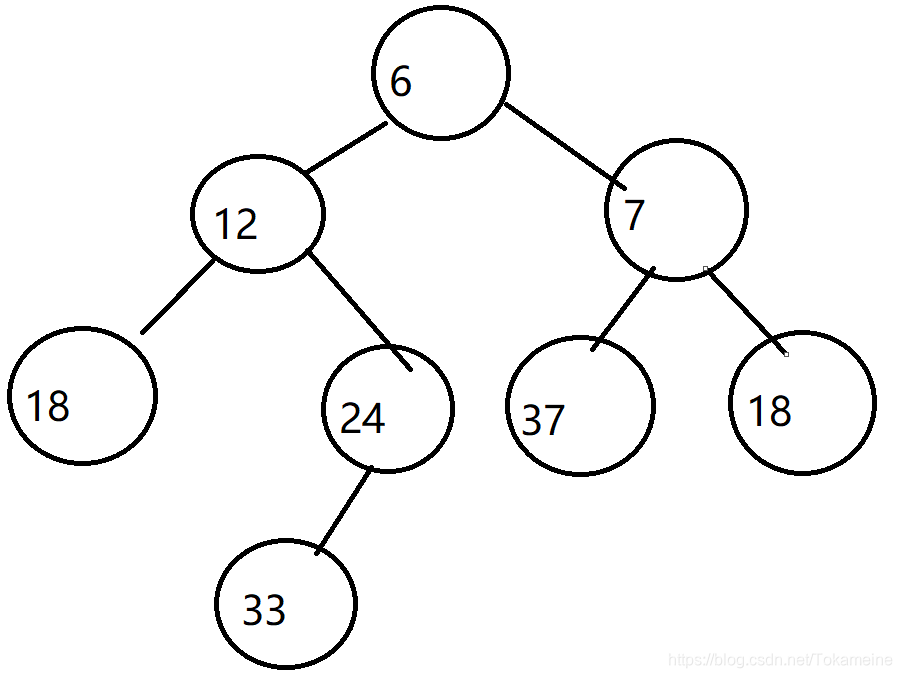
现在,不妨先假设根节点为3的堆为H1,另外一个为H2。现在将它们放入Merge(H1,H2)。注:以下所说的H1和H2是在不停的变动的,具体目标请以所指根节点为准。
经过一系列的比较,达到这行代码:
1
| H1->Right = Merge(H1->Right, H2);
|
①将H1->Right指向 根节点为8的堆 与 H2 合并的结果。
同理,经过一系列的比较。现在,H1的根节点是6,H2的根节点是8。
②再次遇到相同的情况,H1->Right指向 根节点为7的堆 与 H2(根节点为8的堆) 合并的结果。
再次经过一系列的比较。现在H1的根节点是7 ,H2的根节点是8。
③同上,令H1->Right 指向 H1(根节点为18的堆) 与 H2(根节点为8的堆)合并 的结果。
上一行描述合并后的结果显而易见,只是将18放到了8的右儿子处罢了。然后返回新根 8 的地址。
现在,③行处的H1->Right指向新根 8。即 7->8。
判断Npl,并将左右子树进行一次交换。
以上内容实现了 根节点为3的右子树与 根节点为6的堆 的合并过程。
回到①行中方的H1->Right,其现在指向了新的根 6。判断Npl,再次旋转。
合并完成。
很多时候,即便我仔细地捋顺了递归操作的流程,它的可读性仍然相当糟糕……但如果不去捋顺过程,又没办法改进其操作,甚至有的时候连利用都做不到。对于我这种出入数据结构的萌新来说,可能只能多看看代码来适应这种生活吧……
二项队列Binomial Queue:
(以下不只是简介,还包括了一些个人理解,如果您学习过程遇到什么麻烦,不妨先看看)
根据书上的描述,似乎是左式堆的一种改良版。虽然左式堆和斜堆每次操作都花费logN时间,且有效支持了插入、合并与最小值出堆,但其每次操作花费常数平均时间来支持插入。而在二项队列中。每次操作的最坏情况运行时间为logN,而插入操作平均花费常数时间。这算是在一定程度上优化了斜堆。
其结构就如名字一样,是“二项”。我们可以将其简单理解为“上项”和“下项”(这只是为了方便理解罢了,实际运用中自然不存在这种称呼,但我总要找个名字给它,不然描述起来还挺费劲的)。实际的样子当您看到图片的时候就能明白,我为什么要那样称呼它们了。
并且,二项队列的样子也特殊一点。它是一种被称之为“森林”的结构,形象的说,它包括了许多中不同高度的二叉树(但每一种高度的树只有一颗,一旦出现两颗同样高度,它们就会被立刻合并成新的高度,这也是特色之一)。并且,它也有最小堆的特性,关键字的数值随高度递减,每一个根节点的值都比子树中任何一个节点的关键字小。
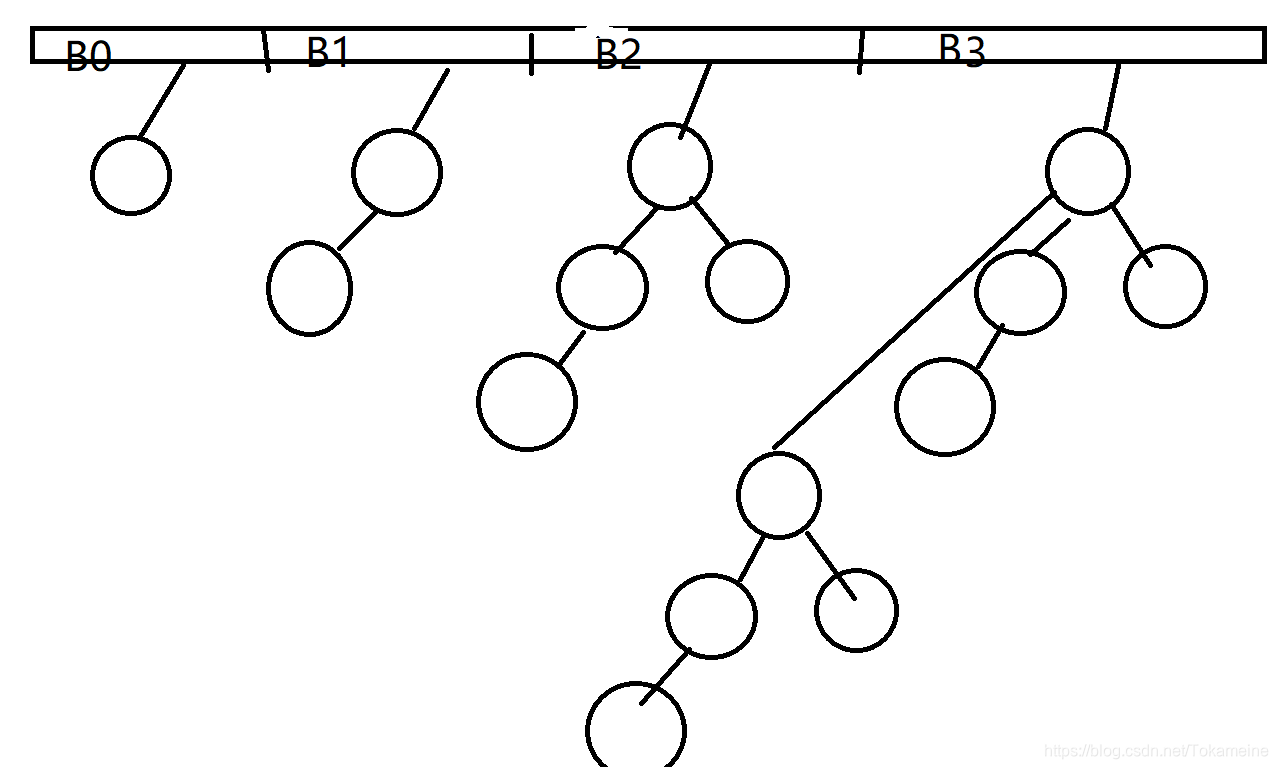
如图,这便算是一个简单的二项队列结构。上面是一个数组,数组中存放有指针。而下面的则是许多的树(剥去数组,你看到的才是真正的二项队结构,数组只是从计算机中实现的一种方法罢了。并且,B3中的那颗树和我们实际实现的有些不同,具体的情况后面会写。但目前,权且当它就长这个样吧(或许这才是本该有的结构,但计算机不方便这样做,所以之后会有另外一个实现的样子))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| //-------------声明部分---------------//
typedef struct BinNode* Position;//位置指针
typedef struct BinNode* BinTree;//树指针
typedef struct Collection* BinQueue;//队列指针
#define MaxTrees 5 //数组的长度,也同时规定了二叉树的高度
#define Capacity ((1<<MaxTrees)-1)//容量是2^0+2^1+......+2^(MAXTREES-1)
BinQueue Initialize(void);//建立空队列
BinTree CombineTrees(BinTree T1, BinTree T2);//合并高度相同的树
BinQueue Merge(BinQueue H1, BinQueue H2);//合并两个队列
int DeleteMin(BinQueue H);
void Insert(int X, BinQueue H);
int IsEmpty(BinQueue H);
struct BinNode //树节点
{
int Key;
Position LeftChild;
Position NextSibling;
};
struct Collection //森林
{
int CurrentSize; //已容纳量
BinTree TheTrees[MaxTrees];//容纳二叉树的数组
};
//-------------声明部分---------------//
|
因为书上没有说明一些变量的作用,所以我自己绕了一会,在这里顺便说明一下吧:
CurrentSize:已容纳量。指的是整个队列的节点数。比方说上图中的的容纳量就是15(对应总共15个节点)。
Capacity:队列容量。指的是一个二项队列结构最高能容纳的节点数。比方说上图的队列容量就是(B3——15)(也因为我画的不太好,所以B3看起来高度不像3,但会意一下就行,实在不行去找找其他大佬的图也行)。(但写法是一个等比数列求和结果,很明显,每个高度的节点数是等比增加的)
LeftChild/NextSibling:连接指针。这个东西具体到后面看见实际的图片时,自然会懂。
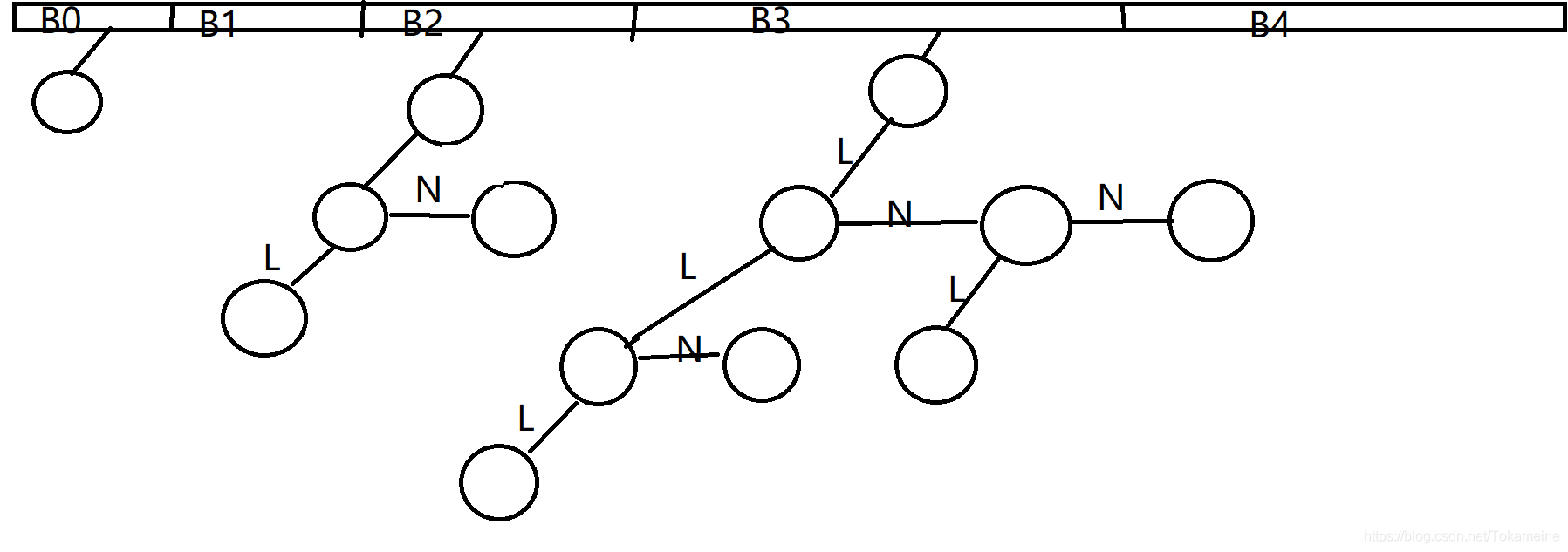
这幅图为实际做出的结构,以下说明的时候请经常对照以方便理解。高度相同的节点我已经尽量画在同一水平线了,也如您所见,B1没有节点,B3的高度确实是3(建立在B0处的节点高度设定为0的基础上)。
关于LeftChild和NextSibling指针已经标出(取首字母表示)。
建立队列Initialize:
1
2
3
4
5
6
7
8
| BinQueue Initialize(void)
{
BinQueue H = new Collection;
for (int i = 0; i < MaxTrees; i++)
H->TheTrees[i] = NULL;
H->CurrentSize = 0;
return H;
}
|
没什么好说的,但因为书上没有,加上我当时不太明白几个参数的作用,所以绕了好一会,贴在这里以防万一。(至少如果不明白CurrentSize是什么,就没办法让它等于0了……)
插入节点Insert:
1
2
3
4
5
6
7
8
9
10
11
| void Insert(int X, BinQueue H)
{
BinQueue temp = initialize();
temp->CurrentSize = 1;
temp->TheTrees[0] = new BinNode;
temp->TheTrees[0]->Key = X;
temp->TheTrees[0]->LeftChild = NULL;
temp->TheTrees[0]->NextSibling = NULL;
Merge(H, temp);
delete temp;
}
|
从这个函数可以看出,所谓的插入节点,实际上是将新节点当作了一个只有B0结构的二项队列,然后将其合并。目前,我们只需要将Merge函数视作一个合并二项队列的函数即可,关于这个函数会在下面讲到。
最小值出队DeleteMin:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| int DeleteMin(BinQueue H)
{
int i, j;
int MinTree;
BinQueue DeleteQueue;
Position DeleteTree, OldRoot;
int MinItem;//ElementType
if (IsEmpty(H))
return NULL;
MinItem=INFINITY;
for (i = 0; i < MaxTrees; i++)
{
if (H->TheTrees[i] && H->TheTrees[i]->Key < MinItem)
{
MinItem = H->TheTrees[i]->Key;
MinTree = i;
}
}
DeleteTree = H->TheTrees[MinTree];
OldRoot = DeleteTree;
DeleteTree = DeleteTree->LeftChild;
delete OldRoot;
DeleteQueue = initialize();
DeleteQueue->CurrentSize = (1 << MinTree) - 1;
for (j = MinTree - 1; j >= 0; j--)
{
DeleteQueue->TheTrees[j] = DeleteTree;
DeleteTree = DeleteTree->NextSibling;
DeleteQueue->TheTrees[j]->NextSibling = NULL;
}
H->TheTrees[MinTree] = NULL;
H->CurrentSize -= (DeleteQueue->CurrentSize + 1);
Merge(H, DeleteQueue);
return MinItem;
}
|
函数本身不算难,但有些冗长。姑且做些说明,但自己写出来是最有效的理解方式。
①一系列将要用到的声明。其中MinItem是将要出堆的Key(因为我设定的Key是int类型),再将MinItem设定为无限大(Infinity)。
②遍历队列数组,选出队列中最小的关键字节点。用MinTree标记其对应的索引,MinItem拷贝其数值。
③将标记好的最小值节点拷贝到DeleteTree与OldRoot,再把DeleteTree指向其左儿子。删除最小值节点。
④将刚才拷贝的左儿子新建到另外一个队列里,设定好相关的数值,最后把两个队列合并。
值得注意的是,for循环是将失去了根节点的堆重新整合到新队列中。这个操作看起来有些抽象,但实际上是可行的。不妨带入B3节点来试探一下,删去了根节点后,它被拆分成了B0,B1,B2三棵树进入新队列了。最开始的那幅图其实很好的说明了问题,那张图的B3有这明显的复制粘贴B2的痕迹,但事实就如描述一样,它们真的就是像复制粘贴一样的结构。所有你可以试着去拆分一下,Bk去掉根节点必然会变成B0,B1,B2……Bk-1颗树。
以及另外一个注意点:
1
| H->CurrentSize -= (DeleteQueue->CurrentSize + 1);
|
其实不太必要在这个地方纠结太久,但以防万一还是说明一下。这行代码减去的数量将在Merge函数中补齐,先后的总节点数差距确实是 1 ,可以自行验证一下。如果缺乏这条函数,Merge将会导致CurrentSize与实际不符。(之所以减去那个量,是因为Merge会补回DeleteQueue->CurrentSize的数量,和这段语句正好相差 1 )
合并队列Merge:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| BinTree CombineTrees(BinTree T1,BinTree T2)
{
if (T1->Key > T2->Key)
return CombineTrees(T2, T1);
T2->NextSibling = T1->LeftChild;
T1->LeftChild = T2;
return T1;
}
BinQueue Merge(BinQueue H1,BinQueue H2)
{
BinTree T1, T2, Carry = NULL;
int i,j;
if (H1->CurrentSize + H2->CurrentSize > Capacity)
exit;
H1->CurrentSize += H2->CurrentSize;
for (i = 0, j = 1; j <= H1->CurrentSize; i++, j *= 2)
{
T1 = H1->TheTrees[i]; T2 = H2->TheTrees[i];
switch(!!T1+2*!!T2+4*!!Carry)
{
case 0://No tree
case 1://only h1
break;
case 2://only h2
H1->TheTrees[i] = T2;
H2->TheTrees[i] = NULL;
break;
case 4://only carry
H1->TheTrees[i] = Carry;
Carry = NULL;
break;
case 3://h1 and h2
Carry = CombineTrees(T1, T2);
break;
case 5://h1 and carry
Carry = CombineTrees(T1,Carry);
H1->TheTrees[i] = NULL;
break;
case 6://h2 and carry
Carry = CombineTrees(T2,Carry);
H2->TheTrees[i] = NULL;
break;
case 7://h1 and h2 and carry
H1->TheTrees[i] = Carry;
Carry = CombineTrees(T1,T2);
H2->TheTrees[i] = NULL;
break;
}
}
return H1;
}
|
最后是关键性的合并函数Merge。这个例程还需要用到CombineTrees函数,用于合并高度相同的树。
函数本身并不是很复杂,用了一个switch来判断情况,这个方式相当有趣,是很值得学习的一种想法。(!!符号似乎是用来判断存在性的(我不太清楚这样描述对不对,所有用“似乎”),若值存在且非0,则返回1,否则返回0)。
以及比较有趣的是for循环的判断条件 j<=H1->CurrentSize 和 j*=2
看起来有些抽象,解释起来也是。
现在的H1->CurrentSize已经是合并结束后的总节点数量了,而这个数量直接关系到for循环需要抵达哪一个高度的数组格。(比如说,我的数组最高能到B20,但现在根本没有那么多树需要存放,最高的树高度只到B5,那如果全都扫一遍,岂不是浪费了很多时间?)
所有才有 j*=2这个条件来制约。如您所见,每个高度的节点数实际上是固定的 2^Bk(2的Bk次方,k指高度,如B0,B1等)。这就涉及到了一些数学关系,所有我就不写这了。只需要捋一捋,我想很快就会发现这神奇的操作(如果最高到B5,那这个for循环进行4次之后,它的 j 就会超出范围导致for循环终止)。
流程其实没必要细讲了,函数写的很清楚了,注释也有,笔记的目的已经达成了,那就到这吧。



