AVL树Insert与Delete函数分析（C++）

文章发布时间:

2021-02-07

最后更新时间:

2024-12-29

插入函数Insert

先放一下代码。因为是照着黑皮书《数据结构与算法分析》学的，所以代码大致和书上的一样，我并没有做太多修改。只是在理解原理的时候有些比较棘手的地方，所以在这里记笔记，方便以后查看。

int max(int n1,int n2)
{
if (n1 >= n2)
return n1;
else
return n2;
}
//取最大值
 
static int Height(position P)
{
if (P = NULL)
return -1;
else
return P->height;
}
//获取高度//只是通过结构内定义的高度去取值，没有测算
 
static position SingleRotateWithLeft(position K2)
{
position K1;
K1 = K2->left;
K2->left = K1->right;
K1->right = K2;
K1->height = max(Height(K1->left), Height(K1->right)) + 1;
K2->height = max(Height(K2->left), Height(K2->right)) + 1;
return K1;
}
//单旋转(左树旋转)
 
static position DoubleRotateWithLeft(position K3)
{
K3->left = SingleRotateWithRight(K3->left);
return SingleRotateWithLeft(K3);
}
//双旋转(左树旋转)
 
static position SingleRotateWithRight(position K1)
{
position K2;
K2 = K1->right;
K1->right = K2->left;
K2->left = K1;
K1->height = max(Height(K1->left), Height(K1->right)) + 1;
K2->height = max(Height(K2->left), Height(K2->right)) + 1;
return K2;
}
//单旋转(右树旋转)
 
static position DoubleRotateWithRight(position K3)
{
K3->right = SingleRotateWithLeft(K3->right);
return SingleRotateWithRight(K3);
}
//双旋转(右树旋转)
 
avltree insert(int X,avltree T)
{
if (T == NULL)
{
//T为空节点
T = new avlnode;//假定空间永远是足够的
T->height = 0;
T->left = T->right = NULL;
T->info = X;
}
if (X < T->info)
{
T->left = insert(X, T->left);
if (Height(T->left) - Height(T->right) >= 2)//事实上等于2才是最合适的
{
if (X < (T->left->info))
T = SingleRotateWithLeft(T);
else
T = DoubleRotateWithLeft(T);
}
}
else if (X > T->info)
{
T->right = insert(X, T->right);
if (Height(T->right) - Height(T->left) >= 2)//事实上等于2才是最合适的
{
if (X > (T->right->info))
T = SingleRotateWithRight(T);
else
T = DoubleRotateWithRight(T);
}
}
T->height = max(Height(T->left), Height(T->right)) + 1;
return T;
}

如果你也有这本书，并且已经看过这一部分关于avl的描述了，那么关于“什么是avl树”以及这些代码的作用至少是明白的，这里我主要是对书中所写的insert函数做些笔记。

因为在树这一节中，很多地方都是通过递归来实现的，不得不承认这是一种非常巧妙的方法，但对于我这种小白来说，阅读和分析递归代码往往会转不过弯（其实更多时候是我懒得动笔，只在脑子里转了几十个循环，最后把自己绕懵了……）

写在前面，书中的element我用int类型的info代替了，我觉得这样会更容易理解（虽然这样做其实也没什么意义就是了）。

-——————————————————————————

Insert过程分析：

首先，这段函数的第一部分用来判断T节点是否存在。但我最开始还在奇怪，因为我们通常都是创建好了一颗空树，然后再进行插入节点的工作，而这里却要判断T节点是否为空。

但可能是书上对这里的解释并不是那么清楚，这里我说一些自己的看法，如果有问题，欢迎指出。

函数中的X代表的就是info，而T则应该输入我们要进行操作的树的根节点地址，毕竟我们也不清楚这个X应该放到树的什么地方。

但值得注意的是，我们是在使用递归来实现这个功能，也就是说，在每一次递归循环中，T节点是不断改变的，它最终会找到我们要插入数据的实际位置，并在这个地方开辟出新的节点，这才是这段函数的作用。

那么关键其实就在于寻址了。找到X应该放置的位置其实并不难，ADT树中也已经说过这种方法，但找到之后，却要按照AVL树的性质来存放数据。

假设，我们通过函数递归，T参数已经来到了NULL的位置，于是这一次的递归中第一次开辟出了新节点。于是我们将新节点的地址返回到了上一次递归中（显然X=T->info，所以其他判断都不起作用了）。

不妨假设我们上一次是向左树去找，大概就是下面这样（没用鼠标垫，所以漂移的有点厉害……）：

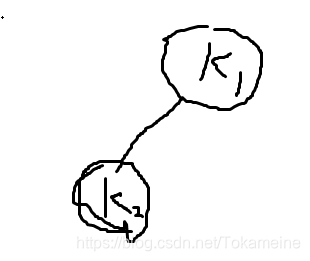
所以这一次，T节点实际上是指K1。

1	`T->left = insert(X, T->left);`

而我们刚执行完这条函数，接下来判断K1节点是否打破了平衡状态。

1	`if (Height(T->left) - Height(T->right) >= 2)//事实上等于2才是最合适的`

（之所以会有这道注释，其实只是我的喜好罢了。因为如果在创建和修改二叉树的时候都有这样的操作，那么左树和右树的高度差值根本不可能超过2，因为一旦达到2就会被重新平衡，但我还是想这样写…..）

假设我们这一次没有打破这个平衡，那么最终我们将会返回K1的地址。

注：这里有个巧妙的地方，

1	`T->height = max(Height(T->left), Height(T->right)) + 1;`

这段函数能够保证每一次插入节点的时候，都能为它获取高度。假设现在有一颗空树，我插入的第一个节点T1就获得了高度‘0’，而再次插入新节点T2的时候，T2的高度是‘0’，而这条代码获取了T2的高度又+1，变成了自己的高度，从而到达了高度‘1’。如果每个节点都通过这个函数来插入，那么深度自然就被设定好了。

假设我们从上一次递归出来，回到了下图这个位置。本次递归中T代表了K3的地址。

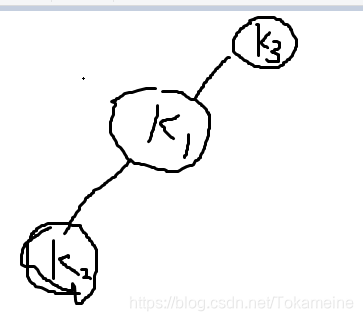
现在，我们通过判断，发现K3打破了平衡状态，于是做了一个奇怪的判断：

1	`if (X < (T->left->info))`

函数在判断X是不是小于K1的关键值。

如果判断为真，其实就说明K2会成为K1的左节点，那么就要进行左树单旋转操作。

如果判断为假，说明K2是K1的右节点，那么就要进行左树的双旋转操作。

（判断左树还是右树，其实是根据K1的位置判断。很简单，所以不再赘述）

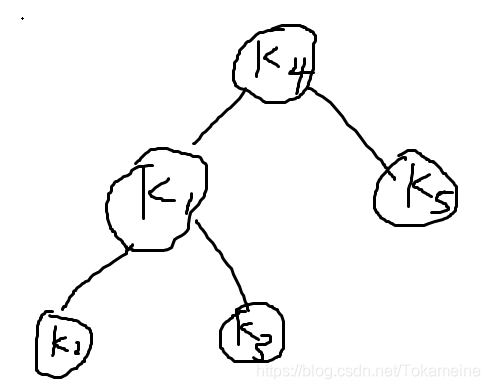
旋转结束之后，返回了K1的地址（这个地址怎么来的，写在左树单旋转函数里了，该函数返回新根）。

假设这一次是平衡的，那么大概会长上图这样了。

最后就是把剩下的还没走完的递归流程走完就行了，这个过程中通常不会再有什么操作了，因为如果你每一次放入节点都用这个函数来操作，基本上都能保证当前的树是一颗正常的树，放入的新节点最多只能影响到它的‘祖父母辈’的平衡状态，只要把‘祖父母辈’的平衡修正回来，通常整棵树都会平衡。

（这个结论是我自己猜测的，如果有错误欢迎指出）

删除函数Delete

先放一下代码：（请注意注释。关于旋转函数，分析insert时贴出过，仅供参考。如果在某个地方没有理解，请先继续往下看一会，或许能找到答案。如果发现代码和解释有问题，请务必指出。）

avltree deletenode(int X, avltree T)
{
//X为删除目标的关键字值
//info为关键字值
position tmp;
if (T == NULL)
return NULL;
else if (X < T->info)
{
T->left=deletenode(X, T->left);
if (Height(T->right)-Height(T->left) >= 2)//height函数用于返回节点所处的高度
{
tmp = T->right;
if(Height(tmp->right)>Height(tmp->left))
T = SingleRotateWithRight(T);//右树单旋转
else
T = DoubleRotateWithRight(T);//右树双旋转
 
}
}
else if (X > T->info)
{
T->right=deletenode(X, T->right);
if (Height(T->left) - Height(T->right) >= 2)
{
tmp = T->left;
if (Height(tmp->left) > Height(tmp->right))
T = SingleRotateWithLeft(T);//左树单旋转
else
T = DoubleRotateWithLeft(T);//左树双旋转
}
}
else
{
if (T->left == NULL && T->right == NULL)//若目标节点没有为叶子
{
delete T;
return NULL;
}
else if (T->right == NULL)//若目标节点只有左子树
{
tmp = T->left;
delete T;
return tmp;
}
else if (T->left==NULL)//若目标节点只有右子树
{
tmp = T->right;
delete T;
return tmp;
}
else//若目标节点左右都有子树
{
if (Height(T->left) > Height(T->right))
{
tmp = findmax(T->left);//找出参数节点中最大的节点，返回地址
T->info = tmp->info;
T->left = deletenode(tmp->info,T->left);
}
else
{
tmp = findmin(T->right);//找出参数节点中最小的节点，返回地址
T->info = tmp->info;
T->right = deletenode(tmp->info, T->right);
}
}
}
T->height = max(Height(T->left), Height(T->right)) + 1;
return T;
}

前提条件：假设现在面对的是一颗完整正确的AVL树，而我们需要对其进行删除节点的操作。

主要思路是运用递归的方法来进行查找，向函数中输入目标节点的关键字以及根节点地址，进行查找。

首先进入递归，函数通过这两条代码以及上面的 if条件语句进行匹配关键字：

1 2	`T->left=deletenode(X, T->left); T->right=deletenode(X, T->right);`

当我们成功找到了这个关键字所在的节点，进入本次递归，此时T节点代表了目标节点。(方便区分起见，我将每个目标节点T称之为T1节点)

于是进入了再往下的环节：判断该节点是否有子树。

情景一：（无子树）

假设该节点是叶，那么它既没有左子树也没有右子树，直接删除该节点，返回NULL值，回到了进入本次递归的函数位子，假设是这一段：

1	`T->right=deletenode(X, T->right);`

那么，T1节点的父节点成功的将本该指向T1的指针指向了NULL，实现了最基础的 ‘叶删除’ 操作。

情景二/情景三：（一个子树）

要么只有左子树，要么只有右子树，这是两个相近的情景，所以何在一起解释。

在每一次的递归中，函数都会创建一个tmp指针用来储存可能必要的信息（你也可以对这个函数进行优化，毕竟不是每一轮递归都需要它，这或许能省下一部分空间）

假设现在我们要删除的目标节点只有一个左子树：

那么我们将tmp指向它左子树的第一个节点，并将这个地址返回，然后T1节点被删除。和情景一相同，它的父节点成功指向了返回值，也就是T1的左子树。

然而需要注意的是，这是在AVL树中的实现。按照AVL树的性质，倘若一个节点没有右子树，那么它的左子树最多也只能有一个节点。所以每个节点对应的高度就有可能发生变化。

1	`T->height = max(Height(T->left), Height(T->right)) + 1;`

因为叶子仍然是叶子，高度仍然为 0 (假设叶子的高度均为0，当然，这只是假设罢了)，于是通过返回的递归右重新测算了改变高度的节点的高度。

至此，删除节点被实现了。

情景四：(两个子树)

最麻烦也最难理解的部分(只是相对而言罢了)。

1	`if (Height(T->left) > Height(T->right))`

他判断了一下目标节点左树和右树哪个比较高，这里不妨先假设一下左树比较高的情景吧。

函数令tmp指向了左树中最大的那个节点，并将该节点的关键字赋予T1节点(实际上是将tmp复制给T1)。

然后进入下一轮递归

1	`T->left = deletenode(tmp->info,T->left);`

注意：这一次，查找的目标关键字变成了左树中最大的那个。

于是我们到达了第二个目标节点T2，并对它进行了删除(这是一个非常简单的删除方法，因为AVL性质规定了数值的大小，只要不停的向右走，走到没有右子树的时候，就能遇见这个最大值，所以这个T2节点一定没有右子树，情景和上面的一样)。

而之所以要找左树中最大的值，是因为进行复制之后，并不会破坏AVL树在数值上的结构：节点左树中的所有值低于节点，右树中所有值高于节点。

最后测算高度，完成了删除节点的工作。

旋转判定：

以上工作只是完成了 ‘ 删除节点 ’ 这一项，但事实上，删除节点之后，还必须面临打破平衡条件的可能性。

回到每一轮递归的入口：(本轮T节点将被称为T3)

T->left=deletenode(X, T->left);
if (Height(T->right)-Height(T->left) >= 2)//height函数用于返回节点所处的高度{
tmp = T->right;
if(Height(tmp->right)>Height(tmp->left))
T = SingleRotateWithRight(T);//右树单旋转
else
T = DoubleRotateWithRight(T);//右树双旋转
}

当我们离开递归之后，必须进行判断是否打破了平衡条件(递归实现了高度的重新测算，这也是非常棒的地方) 。

注：判断条件写了“右树-左树>2”，而并没有包括“左树-右树”的情况。原因是因为：这个路口是指向左树的，也就是说，我们将在左树中删除某个节点。二叉树本身应该保持平衡，倘若现在左树被删除节点，那么左树就不可能比右树要高，所以只需要判断这一种情况即可。在向右查找的过程中也是如此。

假设现在平衡被打破了。也就是说，右树比左树高了 2（其实高度差不可能超过 2 ，但我习惯写成 “>=” 罢了）。

那么该轮tmp将指向T3的右子树第一个节点，然后判断究竟是那一边打破了平衡(必然是比较高的那一边打破平衡)。

假设是tmp的左树更高，那么就需要进行双旋转，如图：（最开始想要删除的节点已经被删除了，造成了如下的情况出现）

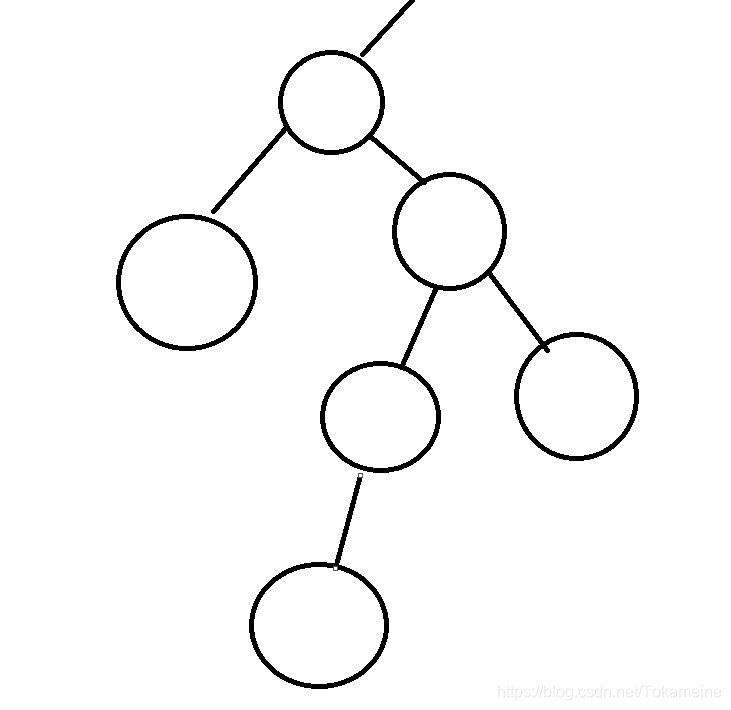
注：

1	`T = DoubleRotateWithRight(T);//右树双旋转`

这些旋转函数都将返回旋转之后的新根。

其他情况也是相同，判断是否旋转，并判断应该选择哪一种旋转。

且在每一轮的递归里，都重新计算了高度。

至此，整个函数完成了删除节点的全部流程。

≡